The Elite Encryption Algorithm (EEA)
Table of Contents:
- Overview
- Background
- Keys & Key Generation
- Encryption Algorithm
- Decryption Algorithm
- Wrapping Things Up
Overview
The Elite Encryption Algorithm (EEA) is a brand new symmetric-key encryption algorithm that utilizes, and takes inspiration from, a variety of cryptographic principles to achieve an elite form of encryption. The Elite Encryption Algorithm takes inspiration from one-time pads and utilizes randomness and variability for its key generation. It also takes inspiration from cipher block chaining (CBC) for its encryption process, using a symmetric-key encryption scheme.
Background
Before diving into how this algorithm works, let's first make sure everyone is up to speed on the terms. While not conventional, I think it is important to define and explain things in such a way that your average Joe can understand what's going on and not only appeal to those in the field of study in which the topic comes from. In this case, those are computer scientists, cybersecurity, and cryptography folks.
As mentioned, the Elite Encryption Algorithm utilizes a symmetric-key encryption process. What does this mean? It means you use the same key(s) to encrypt and decrypt data. This is in contrast to how asymmetric-key, or sometimes referred to as public key, encryption, like RSA, works. Asymmetric-key encryption schemes utilize two keys: a public key and a private key. In the case of RSA, for example, those keys are related based on prime numbers and some fancy math, which allows the public key to decrypt data encrypted by the private key, and the private key to decrypt data encrypted by the public key. The key thing to note, though, is that if you encrypt something with the public key, the public key cannot be used to decrypt that data, and the same thing goes with the private key.
Another cryptographic principle that the Elite Encryption Algorithm takes inspiration from is cipher block chaining (CBC). CBC is a way of encrypting data where you split your data into chunks, or blocks, and with the use of an initialization vector (which is just a fixed length random number), when encrypting the first block, and the previously encrypted block of data, for each subsequent block, XOR's them together, and then XOR's that result with the key. Now you might be wondering, what is XOR? XOR, or exclusive or, is an operation that returns true, or returns 1, if and only if A or B is true, but not both. A good visualization of this can be seen below in Table 1. Now, let's look at an example of XOR in action.
| A | B | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Table 1. XOR Truth Table
In the truth table above (Table 1), you can see the result is only 1, or true, if A is true or B is true, but not when they are both true. Let's say I have two numbers, 9 and 5. Their respective binary values are as follows: 1001 and 0101. If I were to XOR them together, I would have 1100, which is the binary value for 12, as seen below.
1001
XOR 0101
_________
1100
The last major principle is one-time pads. One-time pads are random, single-use keys that are used to encrypt data. These keys also have to be as long as, if not longer, than the data they are encrypting. The reason they are called "one-time pads" is because they are meant to be single-use. They are also known to be uncrackable if utilized correctly.
How does the Elite Encryption Algorithm work: Keys & Key Generation
Now that we are all on the same page, let's break down how the encryption works. Before any encryption can be done, you need to have an encryption key or, in this case, encryption keys. This is where the one-time pad inspiration comes in. While it is not a one-time pad specifically, it takes inspiration from one-time pads, in the sense that the keys that it generates are completely random. Then, after that random number is generated, it is run through either the SHA-256 or SHA-512 hash function. Not only that, but the keys are not a set length either. Keys have the ability to be, at minimum, 256-bits, 512-bits, 1024-bits, or even 2048-bits in length. In the event that 1024 or 2048-bit keys are selected, multiple random numbers are generated and hashed with the SHA-512 algorithm and then concatenated together to form the larger keys.
I should point out, though, with how the actual encryption and decryption algorithms are designed and written, there is nothing stopping you from using keys that are longer than 2048-bits in length. As a matter of fact, all that would need to be done to support this, in my current Java implementation, would be to update the choice boxes used during the key generation process to have options larger than 2048, such as: 4096, 8192, etc. As a matter of fact, my Swift and C implementations supports this use case. Since the algorithm to generate keys, as seen in Figure 1, just keeps generating random numbers and hashing them until it reaches the specified key length. The only restrictions that exist when it comes to the individual key length are that it must be a minimum of 256-bits in length, in which case the SHA-256 hash algorithm is used, or be some multiple of 512. In these cases, as mentioned before and seen in Figure 1, random numbers are hashed with the SHA-512 hash function and concatenated together until that length is met. Lastly, all keys must be the same length; so, for example, if you had five keys for encrypting and decrypting data, you couldn't have two of those keys be 512-bits long and three of those keys be 1024-bits long. The key length cap I put, at 2048-bits in length, in my implementation is completely arbitrary, and the four key lengths I chose were just done to demonstrate the point that you can have keys of different sizes and encryption and decryption still works all the same.
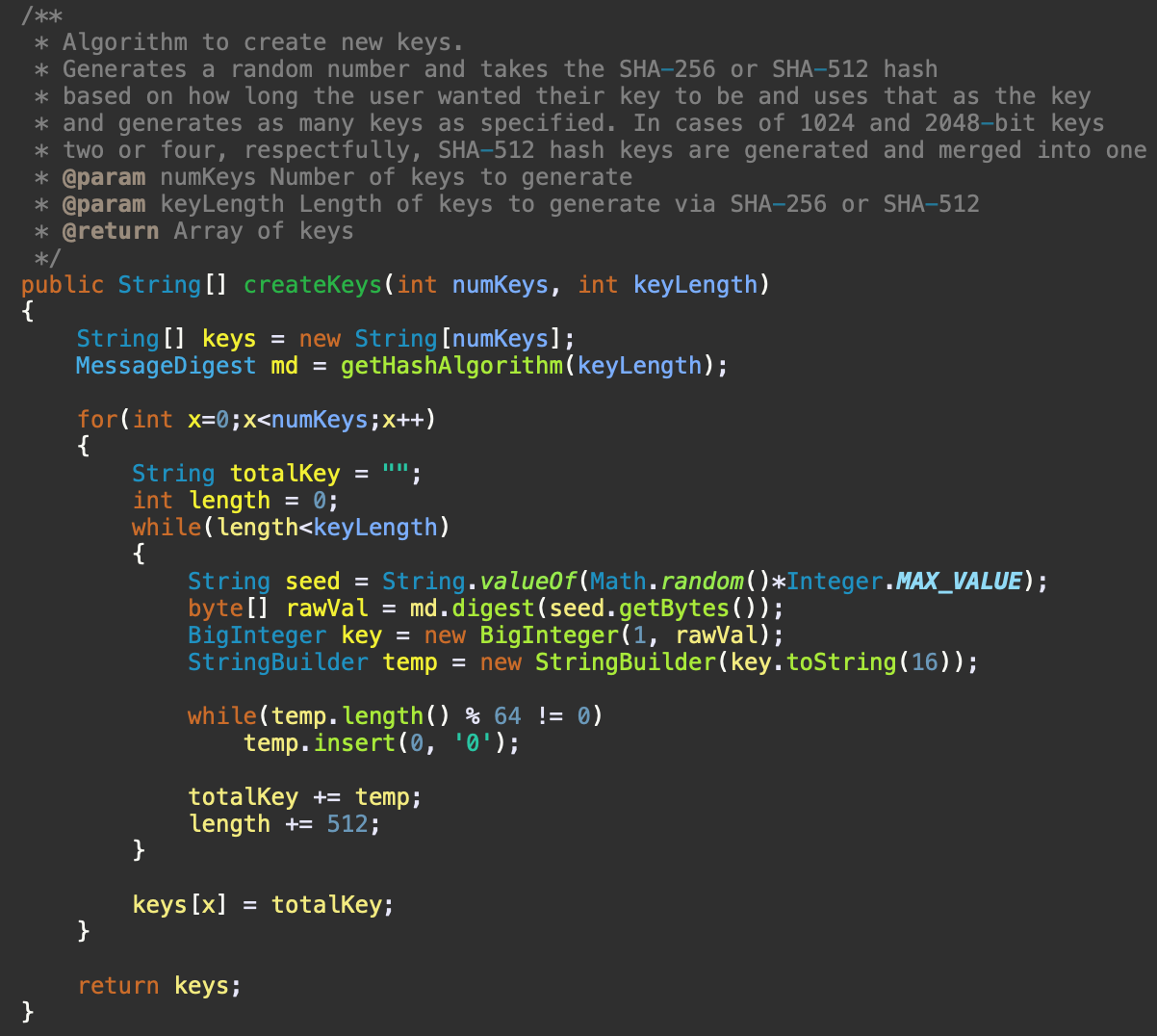
Figure 1. Java source code implementation of key generation
As mentioned with the Swift and C implementations, you aren't restricted to 256-, 512-, 1024-, or 2048-bit keys. In these implementations, you are able to create any size key, as long as it is a multiple of 256. As seen in the Swift key generation implementation (Figure 2), it adds SHA-512 hashes or SHA-256 hashes until the key length is met.
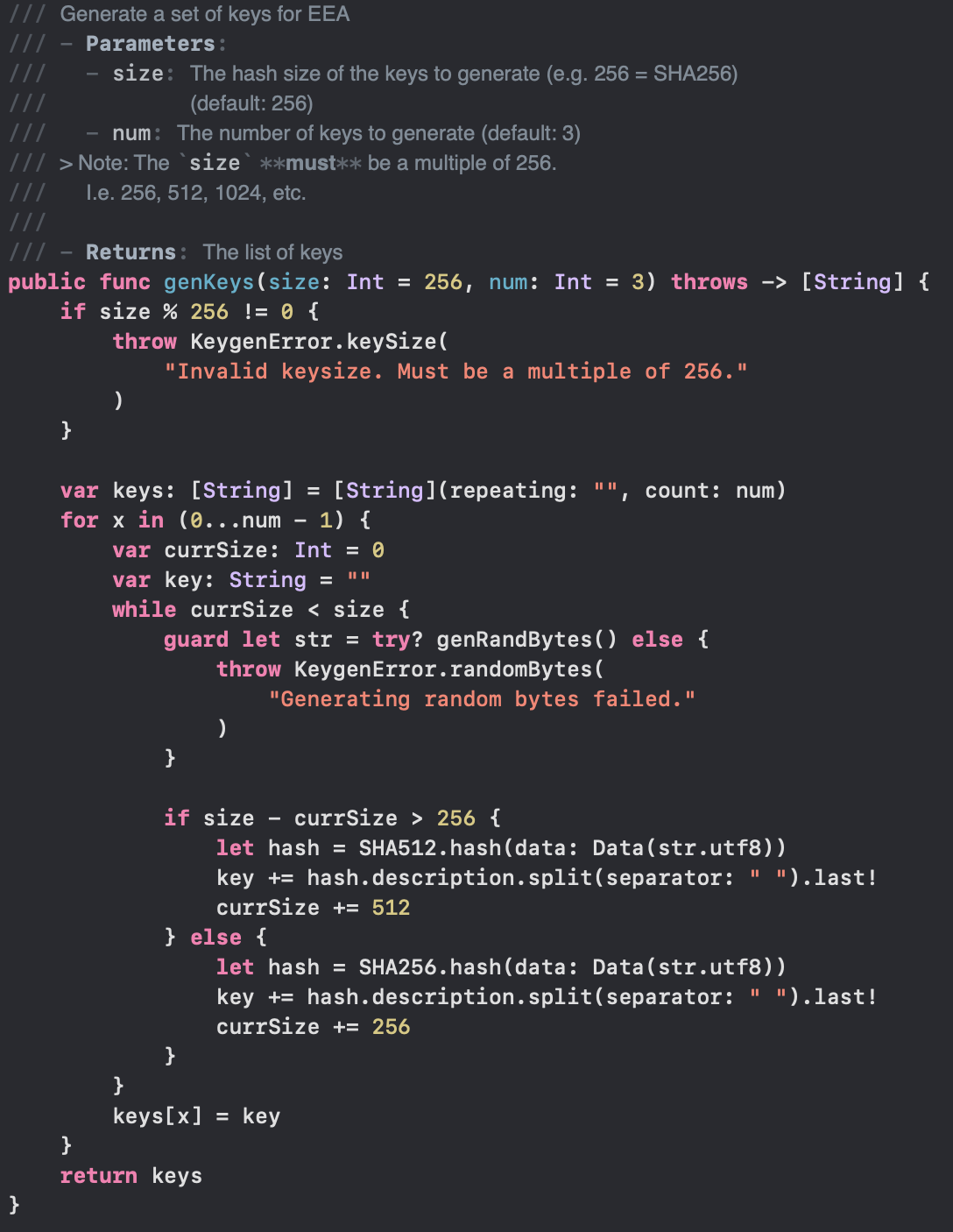
Figure 2. Swift source code implementation of key generation
Even though the Java implementation is restricted to four key sizes, as seen in Figure 3, it is still compatible with keys that are not of one of those four sizes but still meet the requirement of being the sum of multiple SHA-256 and SHA-512 hashes.
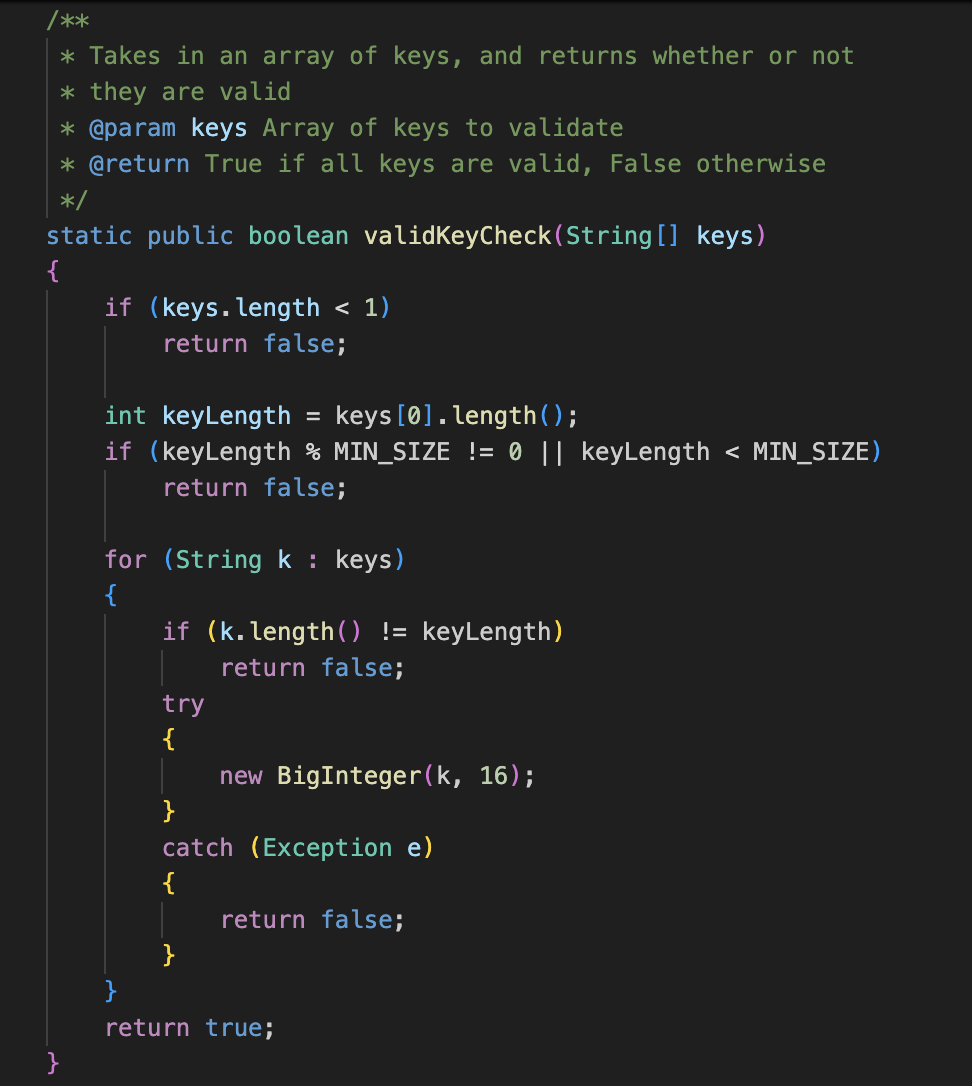
Figure 3. Java source code implementation of key validation
Similarly, as we'll discuss when we talk about how the encryption and decryption is done, the size of the blocks that the data is split into is dynamic. Meaning, the size of the blocks that the data is split into is dependent on the length of the keys passed in. Therefore, the encryption and decryption process have support for keys of any length. Hypothetically, Bob could take my implementation, modify the choice box to be able to select 8192-bit length keys, generate keys, encrypt a message, give Alice the encrypted message along with the keys file, and even though her version can only generate keys up to a bit length of 2048, she would still be able to decrypt Bob's message without issue.
Adding to the variability factor, there is no set number of keys to be used. This means you could have 1 key, 5 keys, 3 keys, 30 keys, etc. There is no limit on how many, or how few, keys you can have. It should be noted, though, that the more keys you have, the harder it will be to crack. In general, though, with all this variability in the number of keys and length of said keys that can be used, it makes cracking the encryption that much harder. This is because anyone trying to crack the encryption doesn't know how long the keys were and how many keys were used because of the variability in length and number of keys. As we'll get into, the reason this matters is because the keys build upon themselves in the encryption process. Meaning, there is no single point of failure. Even if an attacker were to get one of your keys and used it, it wouldn't work since they only have the one key. Similarly, even if they had all your keys, they could still fail to break the encryption unless they used the keys in the exact order. Which means the more keys you use, the harder it would be for an attacker to get that order exactly right. This is in contrast to another symmetric-key encryption algorithm, AES, which only uses one key, so if someone gets the key, you're out of luck.
How does the Elite Encryption Algorithm work: Encryption
Now that we have keys covered, we can get into the algorithms. As seen in Figure 4, encryption is quite simple and looks similar, while also being different, to CBC.
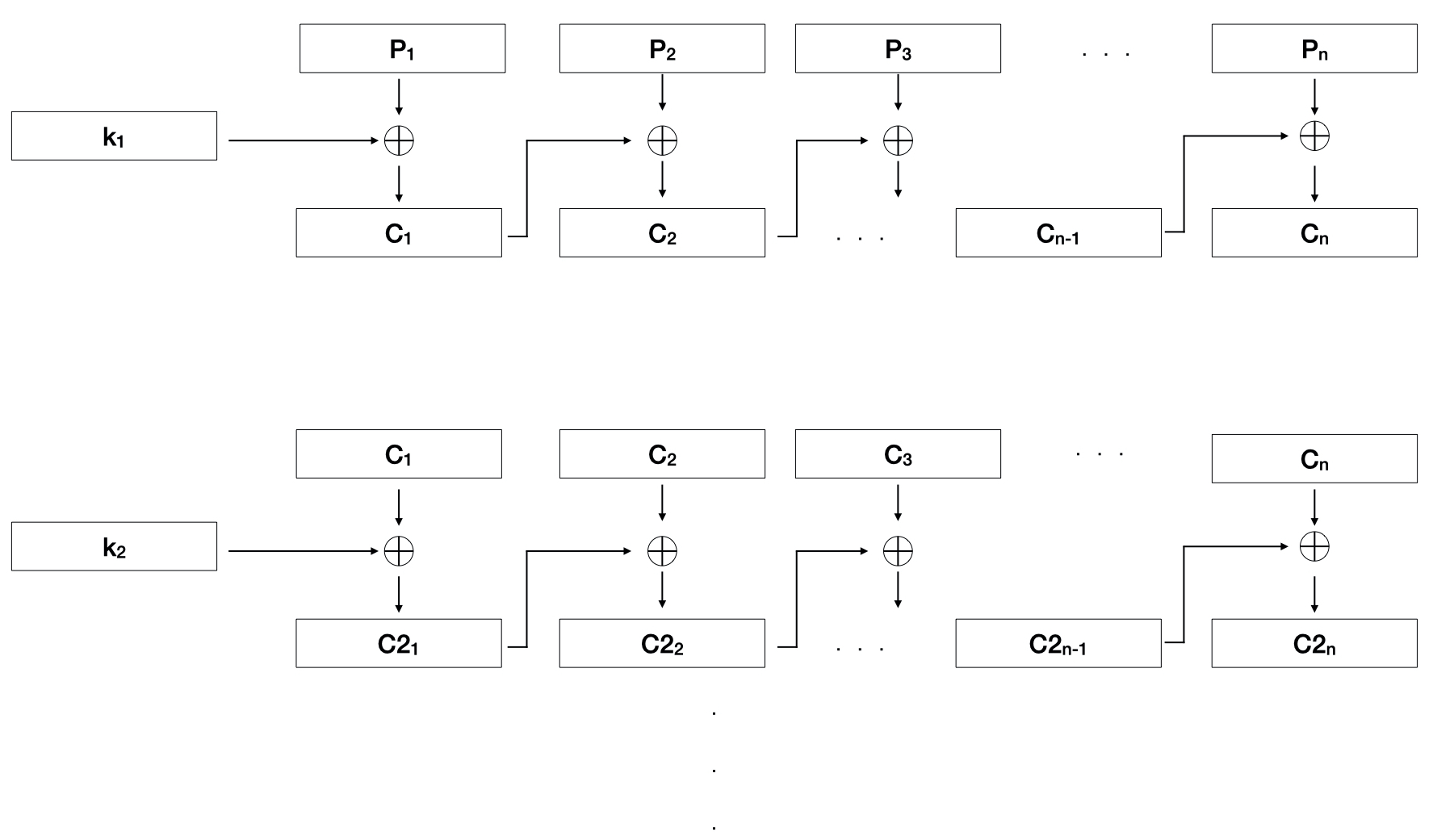
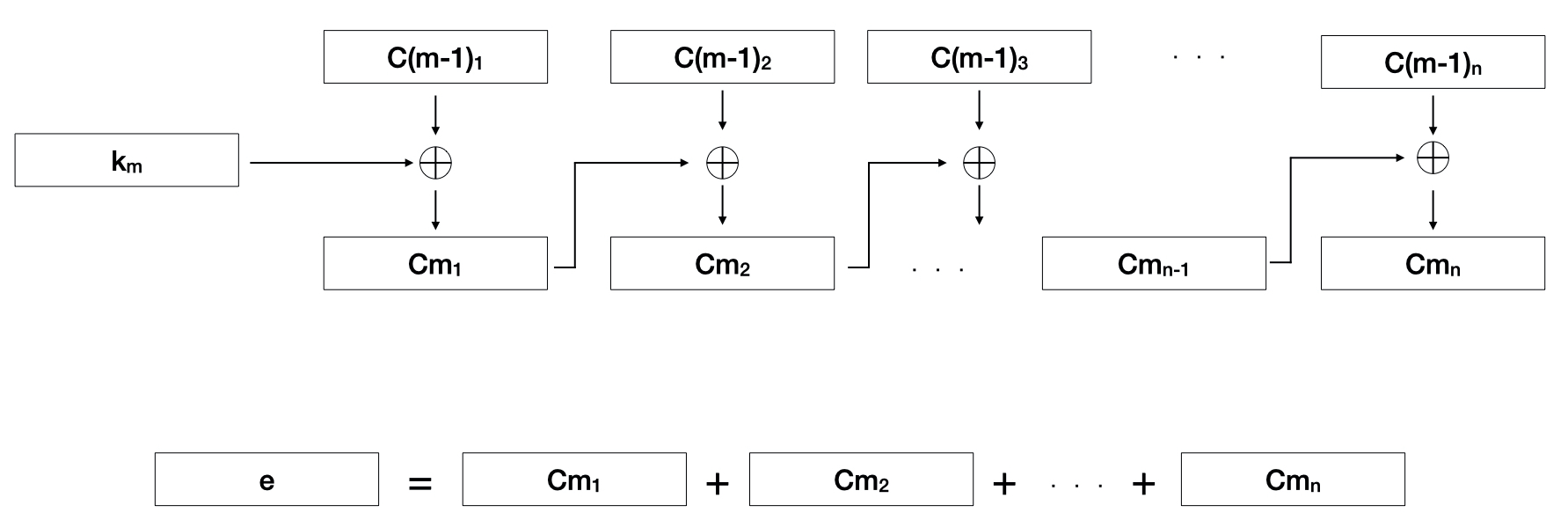
Figure 4. Visualization of the encryption algorithm
The Elite Encryption Algorithm is similar to CBC in the fact that each block of cipher text, denoted by the C's, is used in the XOR process with the next block. The difference is, that the key is only used for the first block of the encryption and no initialization vector is used. As seen in Figure 4, the algorithm is run for as many keys that exist, jumbling the original data more and more with each pass. After all the passes have been completed, the blocks are joined together to create the encrypted data, e.
The size of the blocks is determined by the size of the keys. If the keys have a 512-bit length, then the data being encrypted will be split into 512-bit blocks as well. In cases where the last block is not 512-bits long, excess padding will be added to the end to make it 512-bits in length. As seen in Figure 5 with the Java source code implementation of the encryption process.
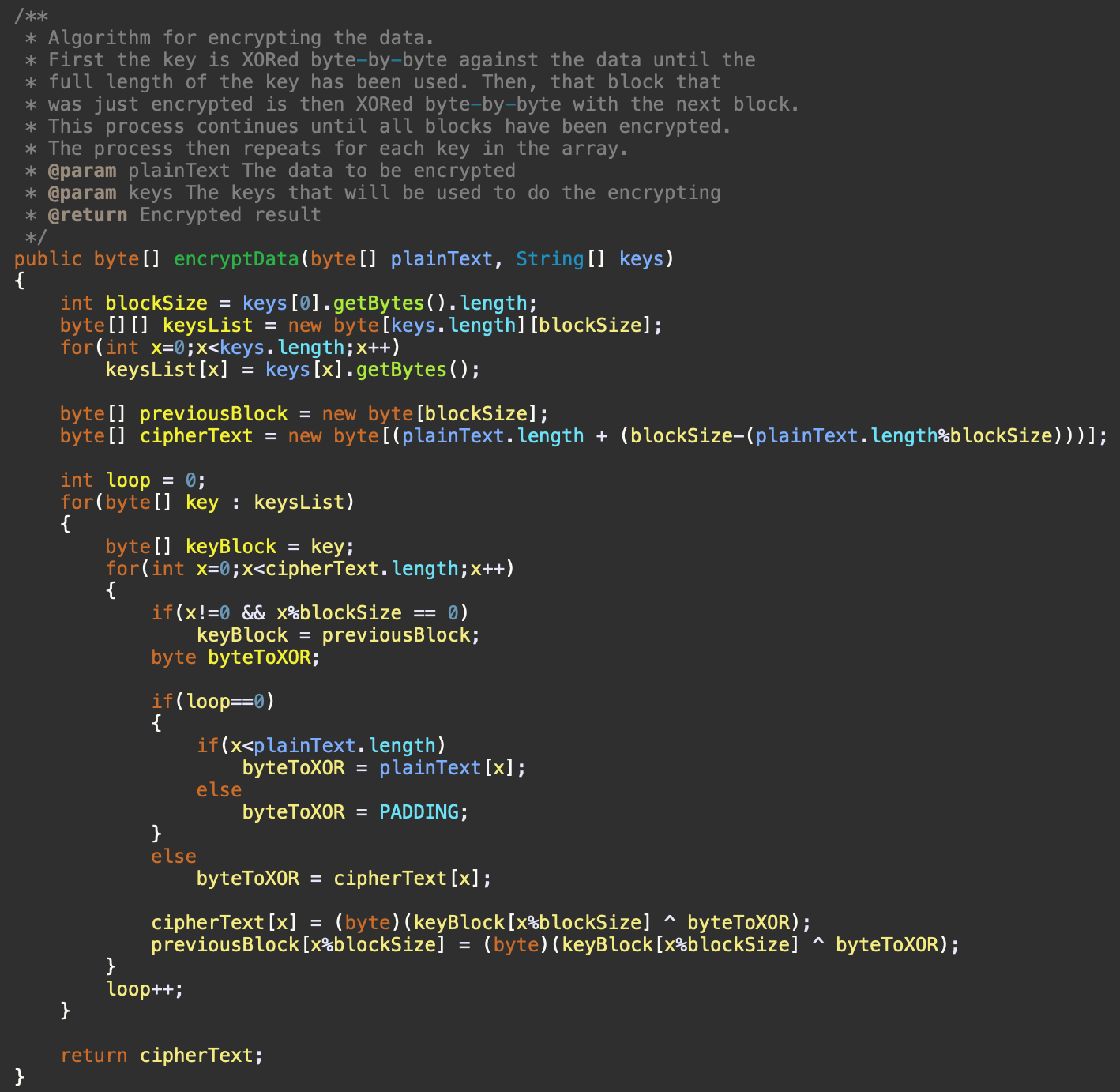
Figure 5. Java source code implementation of the encryption algorithm
How does the Elite Encryption Algorithm work: Decryption
Now that we can encrypt, we have to be able to decrypt our data. This process is, again, quite simple. We just have to do the inverse of our encryption, as seen in Figure 6.
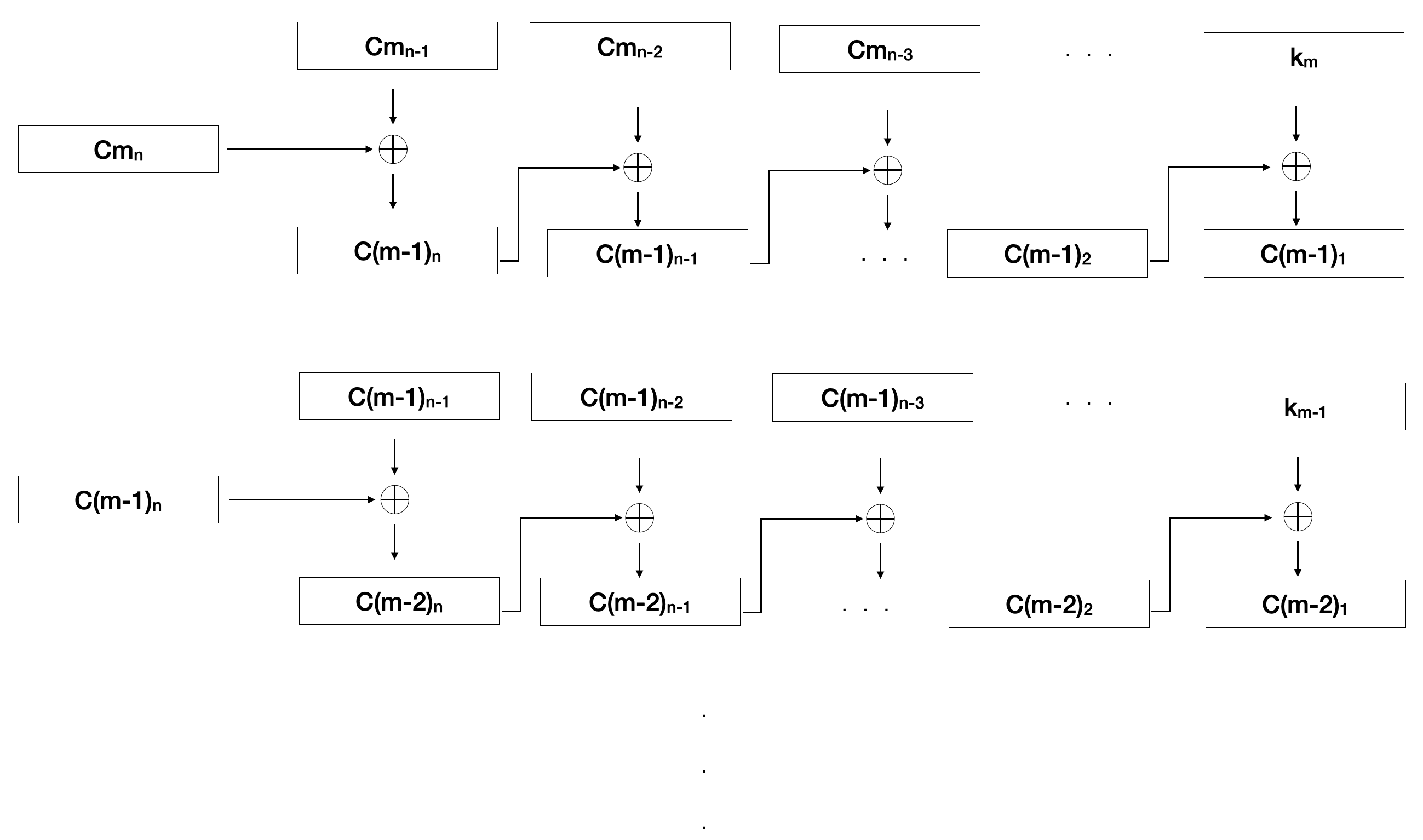
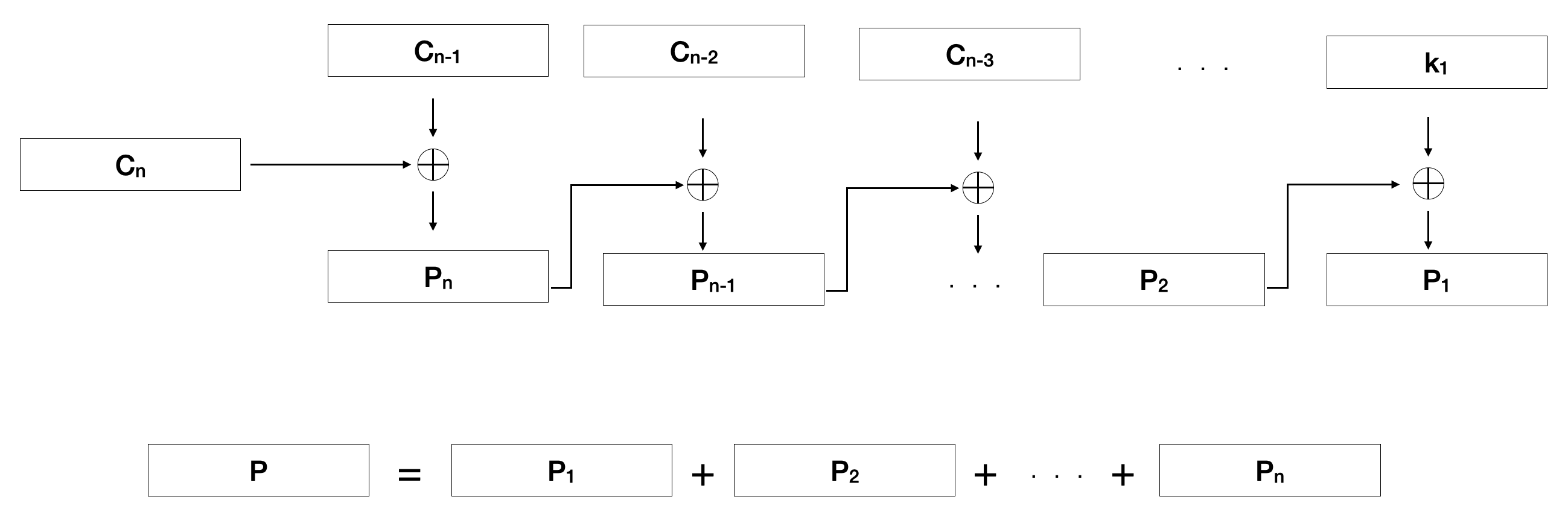
Figure 6. Visualization of the decryption algorithm
Here, we can see we take the second to last block and XOR it with the last block. Then, we take the third to last block and XOR it with the second to last block. We repeat this process until we reach the last block, where we XOR the key with the block. We then repeat this process from the last key to the first key and then concatenate those blocks together to get our unencrypted data, P.
The size of the blocks is determined by the size of the keys. If the keys have a 512-bit length, then the data being decrypted will be split into 512-bit blocks as well. Since the decryption doesn't start with the key, the algorithm has to first determine if the data to be decrypted is long enough. In our 512-bit length example, if the total length is 512-bits and our key is 512-bits, we know only the keys were used; so, we can just XOR with the keys. However, if the length is longer than 512-bits, in this example, we know that not just the keys were used during the encryption and we have to find the second-to-last block in order to decrypt the data. We then continue backtracking until we get to the last block (which is really the first block since we are going in reverse), at which point we use the respective key to XOR against it. We then repeat this process until all keys have been used and the data is decrypted. Once all the decryption is done, any excess padding that was added during encryption will be removed. As seen in Figure 7, with the Java source code implementation of the decryption process.
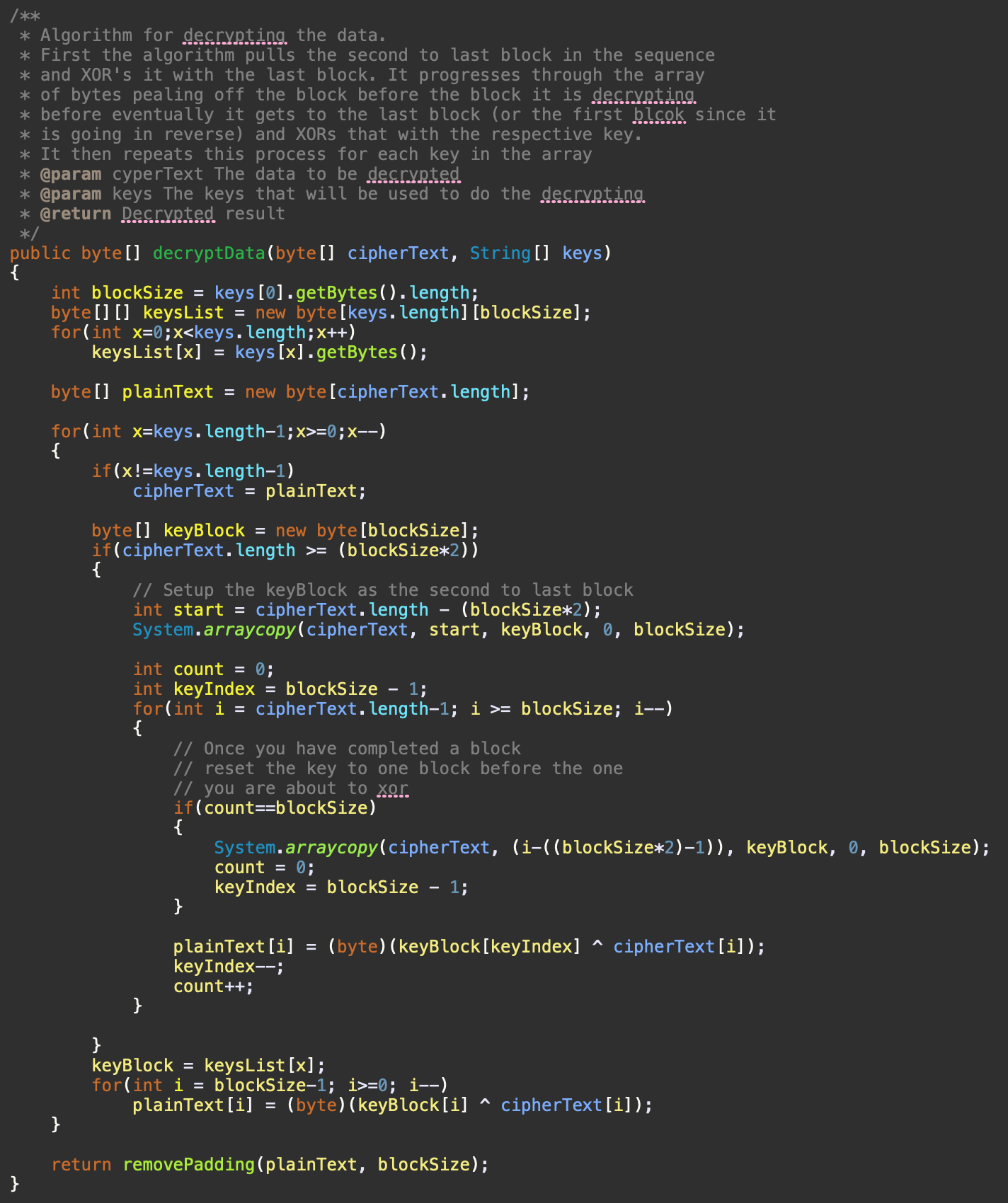
Figure 7. Java source code implementation of the decryption algorithm
Wrapping things up
Should you drop every other encryption scheme you use to utilize the Elite Encryption Algorithm? In short, no. Chiefly, because it has not been certified by the National Institute of Standards and Technology (NIST) like other encryption schemes, such as AES. What this means is that if you use AES, you know your data will be secure, unless an attacker can get a hold of your key. As of the writing of this blog post, the Elite Encryption Algorithm is not certified by NIST. Meaning, that it has not been conclusively demonstrated, and thus certified, that your data is truly secure once encrypted without access to the key(s). However, with that said, because of the cryptographic traits it utilizes and takes inspiration from, in conjunction with all the randomness and variability baked into it, I personally believe it is secure. If, down the line, the Elite Encryption Algorithm gains momentum and does get certified by NIST, or even rejected by NIST, I will be sure to update this blog post to reflect as such; and, I will create a new blog post talking about its certification or rejection.
Regardless of what the future holds for the Elite Encryption Algorithm, I am very pleased with the capabilities it has. It was definitely a fun project and an amazing learning experience for me to dive into the world of cryptography and create something that could actually have a practical purpose in the real world. If you want to see the full source code I referenced in this blog post, you can find it on my GitHub. In addition to seeing the source code for generating keys, encrypting, and decrypting, you'll also find a desktop and command-line applications utilizing the Elite Encryption Algorithm; so, you can start using the Elite Encryption Algorithm to encrypt and decrypt your data. The desktop (GUI) application is written in Java, while the command-line application has two variants. One is written in C and the other in Swift. Over time, as I incorporate this algorithm into other personal projects of mine in the future, I will update the repo to have implementations in other languages.